電気回路回です。
電気回路を解くうえで、(個人の主観で)非常によくお世話になっている重要な法則・定理は下記ですが、これらに対する私の理解を、本稿から数回にわけてまとめていきます。
- オームの法則
- キルヒホッフの法則
- 分圧の法則
- 分流の法則
- 重ねの理
- テブナンの定理
そのうち、本稿はタイトルのとおり、オームの法則についてです。
電気の世界において、まさに基礎中の基礎と呼べる法則です。
これを知らずして電気の世界の面白さを知ることは難しいでしょう。
というか、いつ何時でもオームの法則にお世話になります。とても重要な法則です。
ですが、身構えることはありません。法則そのものはいたってシンプル。
張り切ってまいりましょう。
オームの法則 (Ohm’s law)
電気回路中に流れる電流と、その電流が流れる対象の両端に生じる電位差に関する法則です。
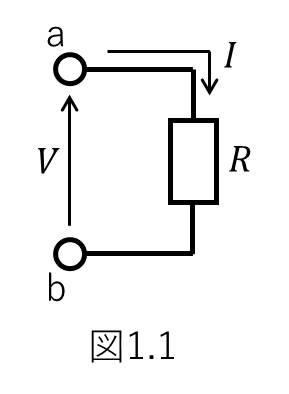
下図1.1に示すような、大きさ\(I\)の電流が流れているシンプルな回路を考えます。
このとき、四角形で示す素子の両端 (a-b間) に生じる電位差\(V\)と電流\(I\)の間には以下の式で示すような関係があります。
\( V=R \times I \)
平たく言うと、電位差\(V\)は電流\(I\)に比例する、ということです。
このときの比例定数Rを電気抵抗 (Electric resistance)と言います。単に抵抗とも言います。
単位は\(\mathrm{Ω}\) (オーム)です。
例1)
図1.1で抵抗\(R=5 \mathrm{[Ω]}\)、流れる電流\(I=2 \mathrm{[A]}\)のときに抵抗の両端に生じる電位差\(V\)は、
\( V = R \times I = 5 \mathrm{[Ω]} \times 2 \mathrm{[A]} = 10 \mathrm{[V]} \)
となります。
このオームの法則、とても便利です。
上の例では電流\(I\)が既知である場合に抵抗\(R\)の両端に生じる電位差\(V\)を求めましたが、電位差\(V\)が既知である場合に電流\(I\)を求める際にも使えます。
例2)
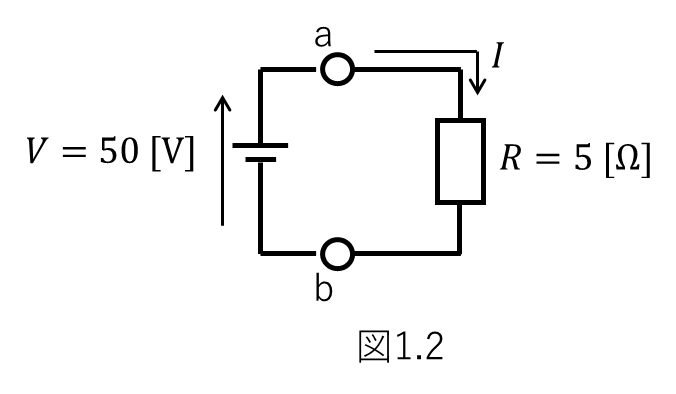
以下の図1.2において抵抗\(R=5 \mathrm{[Ω]}\)に対し、\(50 \mathrm{[V]}\)の電圧を出力する電源を接続したとします。
このときこの回路に流れる電流\(I\)は、オームの法則より、
\( I = \frac{V}{R} = \frac {50}{5} = 10 \mathrm{[A]} \)
となります。
電位差(電圧)\(V\)および電流\(I\)が既知で、抵抗\(R\)の値を知りたいときも同様です。
この抵抗\(R\)、まさにその名のとおり、どれだけ電流を流しにくく(抵抗)するかを示すものです。
例2)において、抵抗\(R\)が倍の\(10 \mathrm{[Ω]}\)だったとしましょう。その場合に流れる電流\(I\)は、
\( I = \frac{V}{R} = \frac {50}{10} = 5 \mathrm{[A]} \)
となり、流れる電流値が半減しました。
このように、抵抗\(R\)の値が大きいほど、その抵抗\(R\)には電流が流れにくくなります。
言い換えれば、この抵抗\(R\)が小さいほど電流は流れやすくなります。
この電流の流れやすさを表す定数を電気伝導率 (コンダクタンス) \(G\)といい、抵抗\(R\)の逆数で示します。
\( G = \frac{1}{R} \)
単位は\(\mathrm{S}\)(ジーメンス)です。
この電気伝導率\(G\)を用いてオームの法則を表すと以下の通りです。
\( I = \frac{V}{R} = \frac{1}{R} \times V = G \times V \)
この式も、見かける機会がそこそこあるので(特に並列回路の問題を解くとき)、頭の片隅に覚えておきたいですね。
直列接続と並列接続
さあ、勉強したオームの法則を使って電気回路を解くんだ!
そう思って、世の電気機器を構成する回路を見てみると……それほど簡単にいかないことが多いのは皆さんご存じのとおりでしょう。
世の電気回路は往々にして複雑怪奇。眺めていると目やら頭が痛くなってきます。
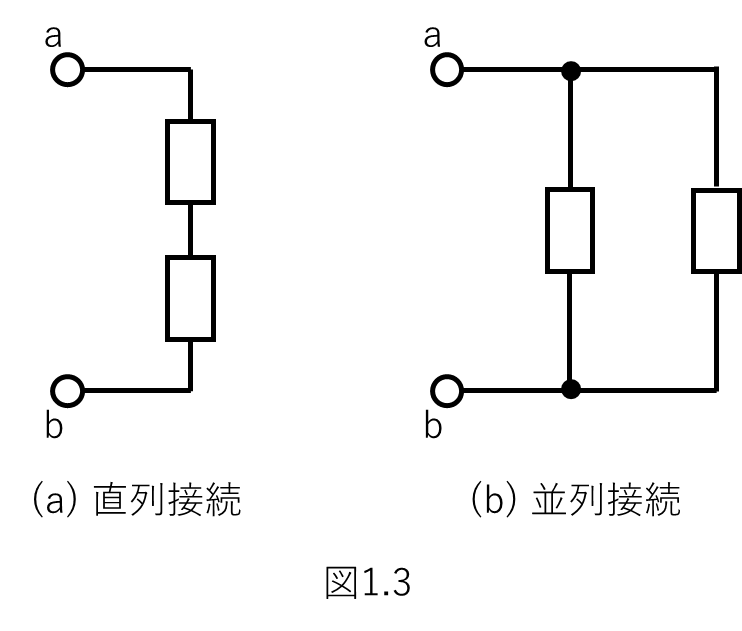
しかしながらその接続の仕方の基本は2種類:直列接続と並列接続です。
下図1.3にその例を示します。左を直列接続、右を並列接続と言います。
これらをオームの法則という切り口から見てみます。
直列接続におけるオームの法則と合成抵抗
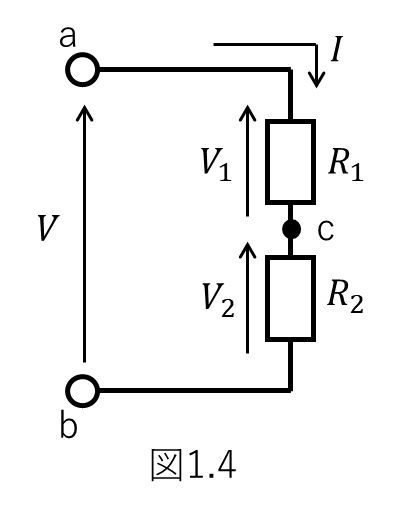
下図1.4を参照ください。
先に示した抵抗1つだけの状態よりも複雑さがレベルアップしましたが、この状態でもオームの法則は使えます。それぞれの抵抗に着目して順番に考えれば良いのです。
流れる電流を\(I\)とします。電流\(I\)の流れる経路はa端-抵抗\(R_1\)-c点-抵抗\(R_2\)-b端となります。
(直列接続のとき、各抵抗に流れる電流は同じ。地味にキーポイントです。)
まずは抵抗\(R_1\)に着目しましょう。その両端に生じる電位差\(V_1\)は
\( V_1= R_1 \times I \)
となります。
次に抵抗\(R_2\)に着目すると、その両端に生じる電位差\(V_2\)は
\( V_2= R_2 \times I \)
となります。
これら2つの抵抗によって生じるトータルの電位差\(V\)はa端-b端間に生じる電位差\(V\)です。これがいくつになるかと言えば、\(V_1\)と\(V_2\)の和になります。
\( V = V_1 + V_2 \)
ところで、トータルの電位差は\(V_1+V_2\)ですが、抵抗\(R_1\)と抵抗\(R_2\)の間のc点とb点の電位差は\(V_2\)です。\(V_1\)分だけ小さくなってます。これは抵抗\(R_1\)によって\(V_1\)だけ電圧が下げられたという見方もできます。
このことから、電流を通電した時に抵抗の両端に生じる電位差のことを電圧降下と表現することがしばしばあります。
すなわち\(V_1\)は抵抗\(R_1\)による電圧降下、\(V_2\)は抵抗\(R_2\)による電圧降下ということです。
英語での記載 (Voltage drop)からドロップなんて言うこともあります。
以上のように、非常に簡単な例で示しましたが、抵抗が3つでも、4つでもやり方は同じです。
このようにそれぞれの抵抗に着目して順繰りとオームの法則を適用することで、各抵抗の両端の電位差、直列接続の抵抗達によってトータルで生じる電位差を知ることができます。
……ひとつひとつ求めていくのは面倒。
そんな声が聞こえてくるようです。わかります。それが人間の性というものです。
それに、先の例では電流が既知の場合でしたが、トータルの電位差が既知の場合で電流を求めたい場合はどうするのか。いずれかの抵抗の両端の電位差がわからなければ電流が求められないじゃないか。
ここで出てくる概念が抵抗値の合成というものです。
例として、先ほど求めたトータルの電位差\(V\)の式を整理してみましょう。
\( V = V_1 + V_2 = R_1 \times I + R_2 \times I = (R_1 + R_2) \times I \)
ここで、\(R_1+R_2 = R\)とおくと、
\( V = R \times I \)
どうですか。このページの一番最初に提示した例のように一つの抵抗を対象としたオームの法則に見えませんか。
これが抵抗値の合成です。複数の抵抗をひとまとめにして扱いやすくできるのです。
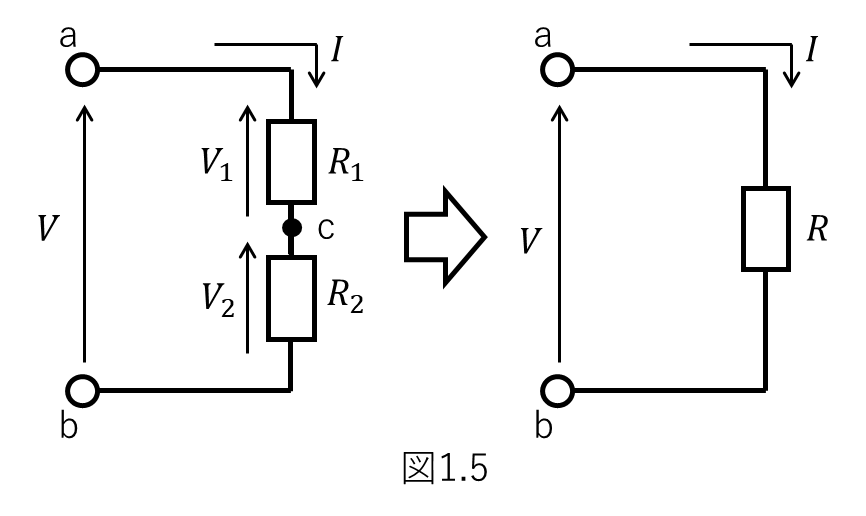
直列接続の合成抵抗を求める場合は、上記の例のように各抵抗値を純粋に足し算すれば良いです。接続する抵抗の数が3つ、4つ…と増えても同様です。
\( R = R_1 + R_2 + R_3 + … \)
……抵抗値を合成できるのはわかってけれど使い道は……?
と思われた方は以下の例をご参照ください。
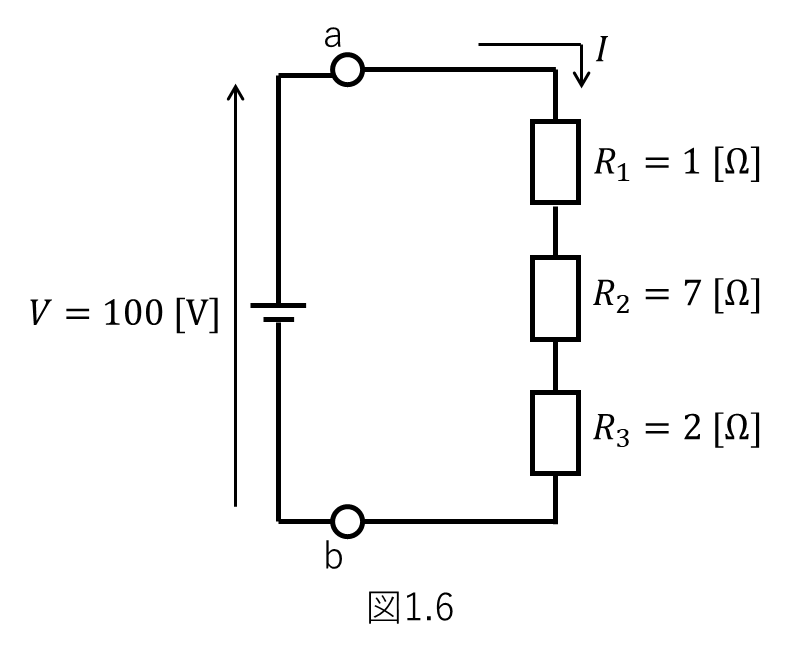
例3)
図1.6に示す回路において、\(100 \mathrm{[V]}\)の直流電源を接続したとき流れる電流値を求めよ。
……例えばこういった問題と対峙したとき、まずすべきは合成抵抗値を求めることです。
直列接続における合成抵抗\(R\)は各抵抗値の和なので、
\( R=1 \mathrm{[Ω]} + 7 \mathrm{[Ω]} + 2 \mathrm{[Ω]} = 10 \mathrm{[Ω]}\)
となります。
これを求めれば、問の答えはもう半分見えています。
いまこの合成抵抗に接続される直流電源の電圧、すなわち合成抵抗の両端に生じる電位差は\(100 \mathrm{[V]}\)なので、オームの法則から、流れる電流Iは、
\( I = \frac{V}{R} = \frac{100 \mathrm{[V]}}{10 \mathrm{[Ω]}} = 10 \mathrm{[A]} \)
となります。
並列接続におけるオームの法則と合成抵抗
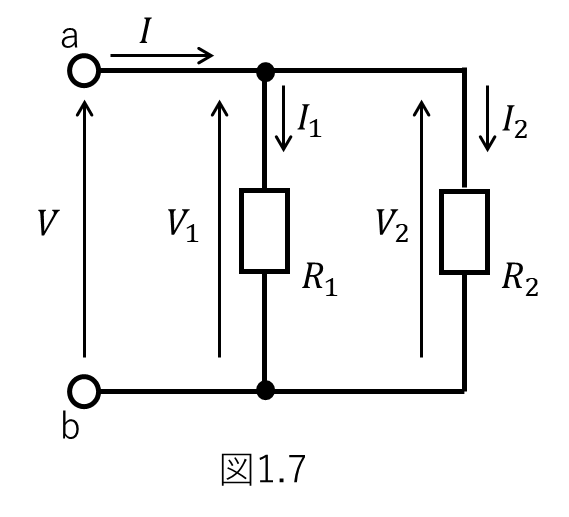
直列接続と同様、並列接続においてもオームの法則が適用できます。
下図1.7を参照ください。抵抗\(R_1\)に流れる電流を\(I_1\)、抵抗\(R_2\)に流れる電流を\(I_2\)とします。また、抵抗\(R_1\)の両端に生じる電位差を\(V_1\)、抵抗\(R_2\)の両端に生じる電位差を\(V_2\)とすれば、
\(V_1 = R_1 \times I_1 \)
\(V_2 = R_2 \times I_2 \)
となるわけです。
ここで、各抵抗に流れる電流値は上式を変形して
\(I_1 = \frac{1}{R_1} \times V_1 \)
\(I_2 = \frac{1}{R_2} \times V_2 \)
で得られますが、この回路にトータルで流れる電流値\(I\)を求めたければ(次の記事のキルヒホッフの電流則を先取りしてしまっていますが)、
\( I = I_1 + I_2 =\frac{1}{R_1} \times V_1 + \frac{1}{R_2} \times V_2 \)
より得られます。
さらにここで、a端-b端間に生じる電位差を\(V\)としてみましょう。
抵抗\(R_1\)の両端が抵抗\(R_2\)の両端にそれぞれ接続され、かつそれらがa端-b端に接続されているので、結局のところ各々の抵抗の両端に生じている電位差、a端-b端間に生じる電位差の関係は
\(V_1 = V_2 = V \)
となります。これを用いると結局トータルの電流\(I\)の式は以下のようになります。
\(I =\frac{1}{R_1} \times V_1 + \frac{1}{R_2} \times V_2 = \frac{1}{R_1} \times V + \frac{1}{R_2} \times V = (\frac{1}{R_1} + \frac{1}{R_2}) \times V \)
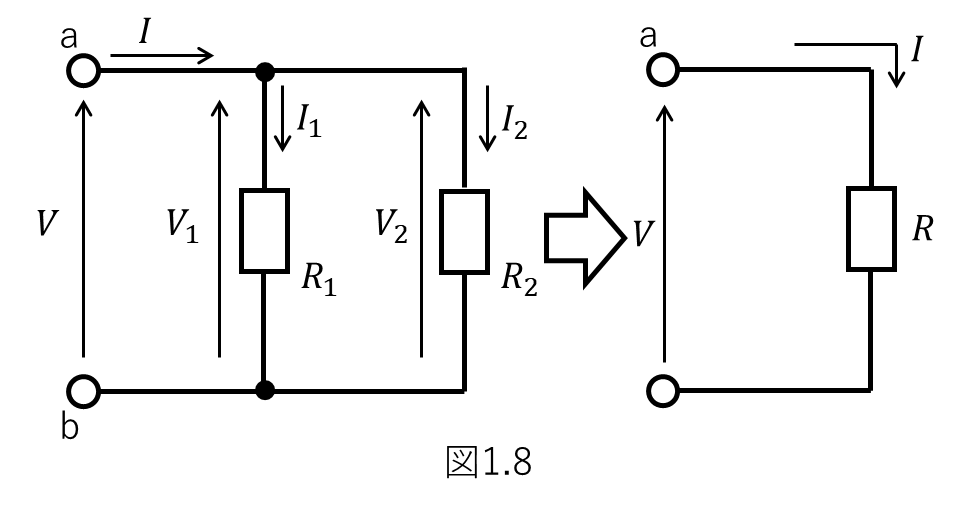
さて、合成抵抗です。
今しがた求めたトータルの電流値\(I\)の式において、
\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \)
と置くと、
\(I = \frac{1}{R} \times V \)
となり、抵抗が一つのときのシンプルなオームの法則と同じ式の形になります。
抵抗が3つ、4つ……と増えても同じです。
\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + … \)
により合成抵抗が得られます。
ところで、電気伝導率で示すと、
\(G = G_1 + G_2 + G_3 + … \)
\(I = (G_1 + G_2 + G_3 + …) \times V = G \times V \)
となり、よりシンプルな足し算の形で式を表現できます。
またこの式を見てわかるように、もし同じ値の抵抗が\(n\)個並列接続されたときの合成抵抗値は、合成前の抵抗値の\(\frac{1}{n}\)となります。
\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_1} + … + \frac{1}{R_1} = n \times \frac{1}{R_1} \)
\(R = \frac{R_1}{n}\)
並列接続において、最も頻繁に遭遇するのは抵抗が2つ並列接続されているケースでしょう。
というか、何個並列に接続されていようとも、そのうち2つに着目して順々に合成していけば最終的には1つの合成抵抗にできます。
なので、2つ抵抗が並列接続されているときの合成抵抗の求め方を覚えてしまうと便利です。
抵抗が2つの場合は、
\( \frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} \)
ですから、これを変形して
\(R = \frac{R_1 \times R_2}{R_1 + R_2}\)
が得られます。
この式は非常によく使います。覚えてしまうのが吉です。式の形状から「和分の積」なんて覚え方もあります。
例4)
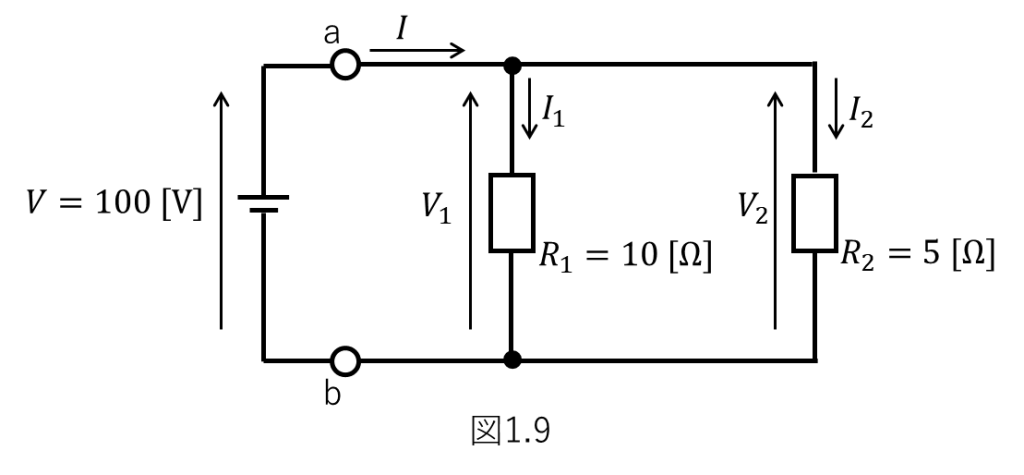
図1.9に示す回路において、\(100 \mathrm{[V]}\)の直流電源を接続したとき抵抗\(R_1\)に流れる電流\(I_1\)、抵抗\(R_2\)に流れる電流\(I_2\)および電流の合計値\(I\)を求めよ。
抵抗\(R_1\)の両端の電位差\(V_1\)および抵抗\(R_2\)の両端の電位差\(V_2\)はいずれも、電源電圧と同じになりますので、
\(V_1 = V_2 = 100 \mathrm{[V]} \)
です。抵抗\(R_1\)、抵抗\(R_2\)それぞれに着目して各電流値\(I_1\)、\(I_2\)を求めると、
\(I_1 = \frac{V_1}{R_1} = \frac{100 \mathrm{[V]}}{10 \mathrm{[Ω]}} = 10 \mathrm{[A]} \)
\(I_2 = \frac{V_2}{R_2} = \frac{100 \mathrm{[V]}}{5 \mathrm{[Ω]}}= 20 \mathrm{[A]} \)
となります。そして流れる電流値の合計\(I\)は
\(I = I_1 + I_2 = 10 \mathrm{[A]} + 20 \mathrm{[A]} = 30 \mathrm{[A]} \)
となります。
上記では各抵抗に流れる電流が問になっていたので、電流\(I_1\)、電流\(I_2\)をそれぞれ求めましたが、トータルの電流だけを知りたい状況もあると思います。そういったときは合成抵抗値を求めてしまうのも手です。この回路の合成抵抗\(R\)は
\(R = \frac{R_1 \times R_2}{R_1 + R_2} = \frac{10 \times 5}{10 + 5} = \frac{50}{15} = \frac{10}{3} \mathrm{[Ω]} \)
よって、トータルで流れる電流\(I\)は、
\(I = \frac{V}{R} = \frac{100}{\frac{10}{3}} = 100 \times \frac{3}{10} = 30 \mathrm{[A]} \)
となり、同じ答えが得られました。
(トータルの電流を求めたのちに、各抵抗に流れる電流を上記とは別のやり方で求めることもできます。分流の法則です。後ほど別記事でまとめます)
総仕上げ
さて、上記の仕上げとして以下の例題にチャレンジしてみましょう。
これが解けたなら、オームの法則を使って色々な電気回路を解くことができるはずです。(きっと)
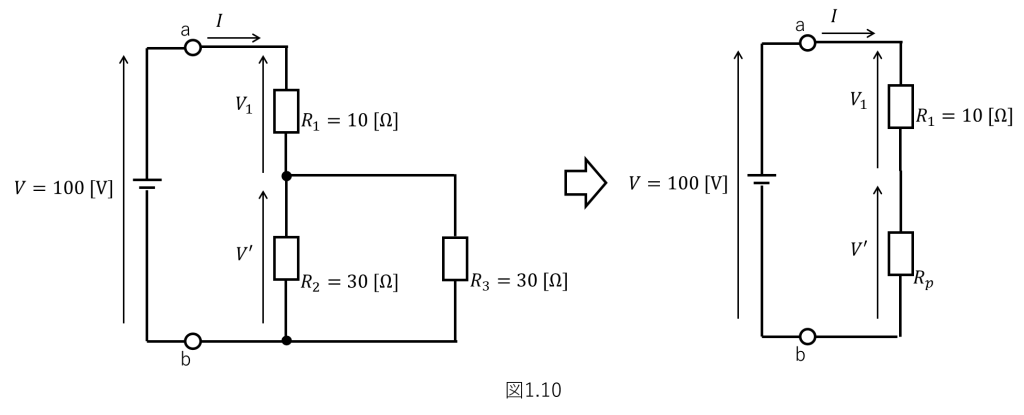
図1.10に示す回路の合成抵抗値Rを求めよ。また、 電流値の合計Iを求めよ。また、各抵抗の両端の電位差を求めよ。
まずは合成抵抗を求めましょう。
まずは並列部分のみ合成抵抗\(R_p\)を求めます。
\(R_p = \frac{R_2 \times R_3}{R_2 + R_3} = \frac{30 \times 30}{30 + 30} = \frac{30}{2} = 15 \mathrm{[Ω]} \)
この\(R_p\)を使って回路図を書き換えてみると、2つの抵抗が直列抵抗された回路になりました。
さらにこれを合成すると、結局この回路の合成抵抗値\(R\)は、
\(R = R_1 + R_p = 10 + 15 = 25 \mathrm{[Ω]} \)
となります。
そして、流れる電流値の合計\(I\)は、
\(I = \frac{V}{R} = \frac{100 \mathrm{[V]}}{25 \mathrm{[Ω]}} = 4 \mathrm{[A]} \)
となります。
電流が求められたので、次は各抵抗の電位差を求めましょう。
抵抗\(R_1\)の両端の電位差\(V_1\)は、
\(V_1 = R_1 \times I = 10 \mathrm{[Ω]} \times 4 \mathrm{[A]} = 40 \mathrm{[V]} \)
となり、また抵抗\(R_2\)および\(R_3\)の両端の電位差\(V’\)は電源の電圧\(V\)と抵抗\(R_1\)の両端の電位差(抵抗\(R_1\)の電圧降下\(V_1\))から、
\(V’ = V – V_1 = 100 – 40 = 60 \mathrm{[V]} \)
となります。
ちなみに、先ほど求めた並列接続部分の合成抵抗\(R_p\)を用いて、
\(V’ = R_p \times I = 15 \mathrm{[Ω]} \times 4 \mathrm{[A]} = 60 \mathrm{[V]} \)
となり、同じ値が得られます。
*
本稿は以上となります。いかがでしたでしょうか。
少しでも電気の楽しさが伝えられたなら幸いです。
次の記事はキルヒホッフの法則です。お楽しみに。


コメント